Type VI Sums of Squares

Products	Versions
Spotfire Statistica	12.5 and later

Description

STATISTICA’s ANOVA calculations use Type VI Sums of Squares with the Sigma-Restricted parameterization by default.

Issue/Introduction

Type VI Sums of Squares

Resolution

Sometimes it can be difficult to understand how and why that output differs from the Type III sums of squares output.

In many cases, Type III and Type VI sums of squares results are the same. The difference arises when there are missing combinations of the predictor variables, and an interaction term is present in the model.

For example, open Characteristics.sta and run an ANOVA analysis with Height as the response variable, and Eye Colour and Hair Colour as the explanatory variables. Accept all default options, including Type VI sums of squares, and display the results.

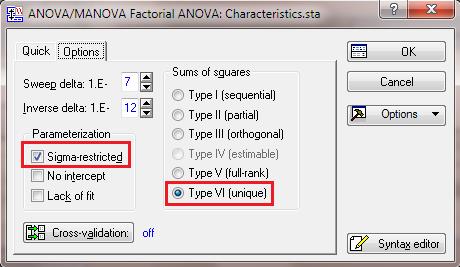
Notice there are no results for Eye Color.

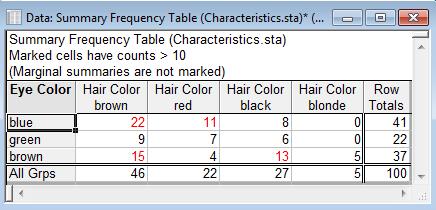
To see why, select Statistics | Basic Statistics | Tables and Banners, and summarize the number of data points for each combination of Eye Color and Hair Color:

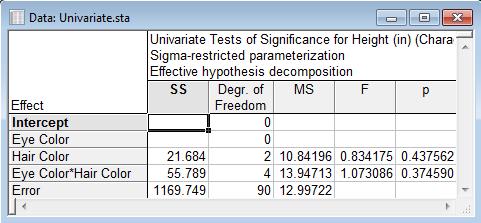
Notice there are are no height data for people who have blonde hair and blue or green eyes.

The presence in the model of an interaction between eye colour and hair colour implies that the effect of a change in eye colour will be different depending on the hair colour. So we cannot estimate the effect of an eye colour change for blondes by using the effect of an eye colour change for those with other hair colours.

In this case, the Type VI philosophy says that because there is only complete data (from all hair colours) for subjects of one eye colour(brown), we cannot compare one eye colour with another across all hair colours. Therefore we will not even try to estimate the eye colour effect.

Notice that we do have complete data (from all eye colours) for multiple hair colours. For instance we can compare the effect of a change in hair colour from brown to red across all eye colours. So we can estimate the hair colour effect. That is why the Type VI sums of squares output includes results for hair colour.

The Type III philosophy is a little different. It says that even though we do not have data for all hair colours across multiple eye colours, we still have data for some hair colours across multiple eye colours. Specifically, we have data for brown, red, and black hair across all 3 eye colours. So we will estimate the eye colour effect using the data where multiple eye colours are available across all hair colours.

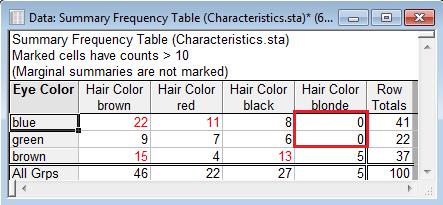
The Type III results are:

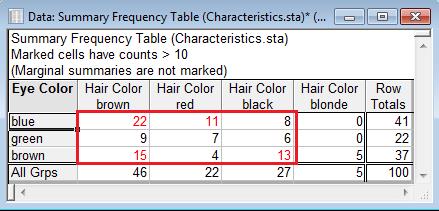
Notice there are results for eye colour and hair colour.

In STATISTICA you can calculate the Type III eye colour effect by de-selecting the sigma-restricted parametrization option, and selecting the Type III option:

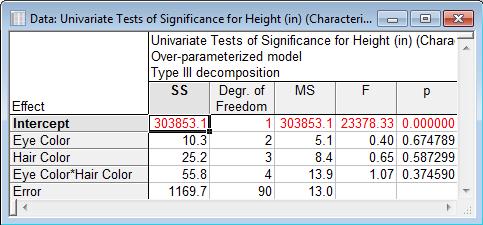
It is helpful to understand how the Type VI calculations are related to the Type III calculations “under the hood”. Remember, the Type VI philosophy is unhappy that among all blondes, there is only data for those with brown eyes. But what happens if we remove those 5 cases from the data?

The blondes are omitted completely from the analysis.

Now we have data for multiple eye colours across all hair colours in the data set. So we can calculate Type VI results for eye colour.

Now the Type VI results are:

And the Type III results are:

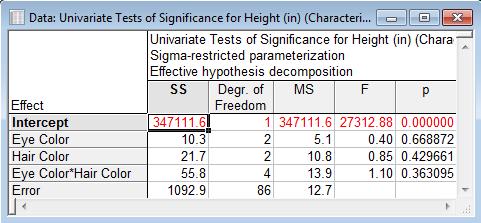
Type III and Type VI results are the same.

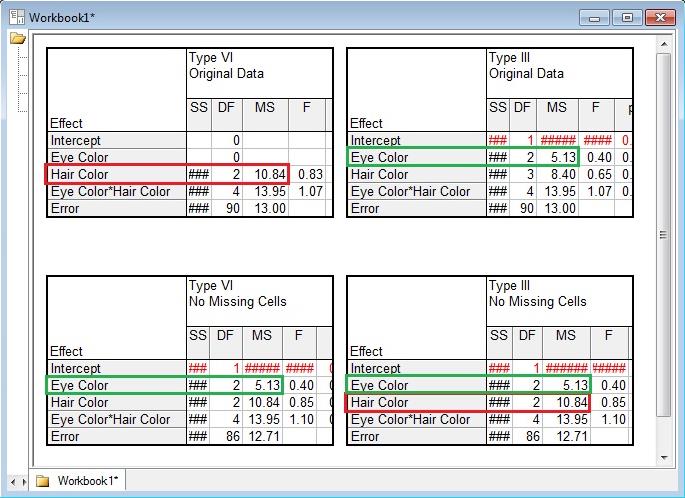
Now let’s compare results for both types of sums of squares, for both data sets:

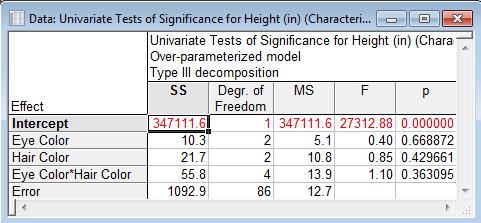
Notice the Type VI hair colour results (in red) for the original data is the same as the Type III hair colour results for the modified data. So that’s what Type VI was doing with the original data: it was ignoring the blondes because they did not have data for multiple eye colours, then doing the usual Type III calculation for hair colour with the non-blonde data.

Also notice the Type III eye colour results (in green) for the original data matches the Type III and Type VI eye colour results for the modified data. So that’s what Type III was doing with the original data: it was just doing the usual Type III calculation for eye colour using the non-blonde data.

Here is a summary of what we learned:

Type VI vs. Type III

Eye Colour:

TypeVI = No results because no data for multiple eye colours across all hair colours

Type III = Use non-blonde data where there is data for multiple eye colours across all hair colours

Hair Colour:

Type VI= Use non-blond data where there is data for multiple hair colours across all eye colours

Type III = Use non-blond data where there is data for multiple hair colours across all eye colours

Welcome to "KB Articles"